How SQL Server stores data types: integers and decimals

This week we’re going to look at how numbers are stored. This post will cover integers (TINYINT, SMALLINT, INT, BIGINT), and decimals (DECIMAL, which is the same as NUMERIC).

If you’d like to read the previous posts in this series of how SQL Server stores data types, here’s what we’ve covered:

• Bit columns
• Dates and times

As a general reminder, there are eight bits in a byte.

Integers

As we know from before, integers are whole numbers, or numbers with no fractions (i.e. no decimal places). This is going to be in the test later, so pay attention. In other words, the numbers 0 through 9 are integers, but a floating point or decimal / numeric value is not an integer. As soon as you add decimal places, it stops being an integer even if the fraction equates to zero.

Inside the storage engine, integers are mostly signed values (they can have negative values), and each integer data type has a fixed size. The exception is TINYINT which only has positive values. Like many other data types, integer types are stored byte-reversed (known as little-endian).

Type	Size	Decimal range	Binary range
TINYINT	1 byte	0 to 255	0 to 2^8 – 1
SMALLINT	2 bytes	-32,768 to 32,767	-2^15 to 2^15 -1
INT	4 bytes	-2,147,483,648 to 2,147,483,647	-2^31 to 2^31 – 1
BIGINT	8 bytes	-9,223,372,036,854,775,808 to 9,223,372,036,854,775,807	-2^63 to 2^63 – 1

Integers are accurately represented in binary. For instance, the number 625 is represented in binary as 00000010 01110001, or 0x0271 in hexadecimal. We use hex as a representation of binary to save space when displaying binary values, but it’s purely at the presentation layer. Every byte is always eight bits wide. A byte is represented by a 2-digit value in hexadecimal. 271 (the hex equivalent of 625) is more than one byte, so we put a leading zero in front of it to round it up to the nearest byte, and use those two bytes to store the value.

625 is ten bits wide, so it is too large for TINYINT‘s boundary of eight bits in the below example. For the rest though, it will look pretty much the same, just with extra zeroes padded to the right. Let’s take a look:

Type	Value	Hex
TINYINT	255	0xFF
SMALLINT	625	0x7102
INT	625	0x71020000
BIGINT	625	0x7102000000000000

Negative values use two’s complement, which we covered briefly last time. It uses the high end of the byte range to store those negative values, starting at -1.

The smallest negative value (-1) has the largest possible hex value (0xFF for each byte), and then counts backwards from there to the lowest possible value. So for the SMALLINT data type, -1 is 0xFFFF, and -2 is 0xFFFE (which is stored as 0xFEFF byte-reversed). The binary values converge at the maximum positive value, where SMALLINT‘s maximum is 32,767 (0x7FFF, but stored as 0xFF7F) and -32,768 is 0x8000, but stored as 0x0080.

Two’s complement is a common technique for storing signed integers to make the best use of the available bytes, and it is why understanding data types is extremely important when converting between signed and unsigned values, and casting between different data types. Endianness certainly complicates matters.

Fixed-precision numerics

In SQL Server, the precision and scale of a DECIMAL (the same thing as a NUMERIC) data type matters a great deal. As far as SQL Server is concerned, DECIMAL(19,4) is a different data type to DECIMAL(18,5), and is stored differently.

As we discussed in a previous post, the precision is the total length being stored including the decimal places, while the scale is the number of digits after the decimal point. So for example, DECIMAL(19,4) has a precision of 19 and a scale of 4, which means it can store up to 15 digits before the decimal point, followed by up to four digits after the decimal point. If a number with more decimal places is stored in that data type, it will be rounded up.

The precision affects the number of bytes required to store the value, ranging from 5 bytes (precision 1 – 9) to 17 bytes (precision 29 to 38). If 17 bytes sounds like a lot, that’s because SQL Server needs to maintain the accuracy for those high-precision values, especially when it comes to financial and statistical calculations.

If you need to know what value is being stored in a column, the scale is the incrementing value. For a decimal column with a precision of 19 and scale of 4, it will require nine bytes to store the amount. The bytes are stored in reverse (little-endian), and the value will increment in 0.0001 increments (the scale of 4), which looks as follows:

Value	Hex
0.0000	0x010000000000000000
0.0001	0x010100000000000000
0.0002	0x010200000000000000
0.0003	0x010300000000000000
625.0000	0x01105E5F0000000000
3000000000.0000	0x0100E057EB481B0000
3000000000.0001	0x0101E057EB481B0000
–3000000000.0000	0x0000E057EB481B0000
–3000000000.0001	0x0001E057EB481B0000

Notice that positive values have 0x01 in the first position, while negative values have 0x00 in the first byte position. Other than that, positive and negative values are identical. This is different to the use of two’s complement in other data types.

Let’s check out the 3 billion value, and remove the leading signed bit: 0x00E057EB481B0000. To look at it in a hex calculator, we need to reverse it to 0x 1B 48 EB 57 E0 00. Putting that into a hex calculator gives us 30,000,000,000,000. Knowing that the scale is 4, we move the decimal point four spaces to the left, and we have our expected value of 3 billion.

The CAST AS VARBINARY problem

The data type on disk makes sense as a byte-reversed integer, because the table definition contains the column information in the metadata. However when we cast a DECIMAL as VARBINARY, things look very different. That’s because — like with the TIME and DATETIME2 data types — the precision and scale needs to be encoded in the binary value to ensure the accuracy is retained.

The bottom line is that you cannot assume that the value you see in a VARBINARY cast is how that value is stored on disk.

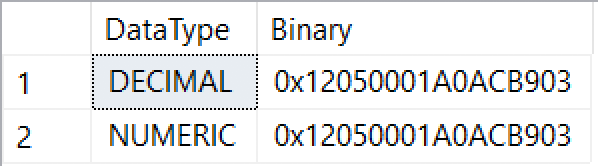
That said, I keep saying that DECIMAL and NUMERIC are the same thing, so let’s prove it with some Transact-SQL that returns the values as binary data in hexadecimal format:

SELECT 'DECIMAL' AS DataType, CAST(CAST(625 AS DECIMAL(18, 5)) AS VARBINARY(25)) AS Binary
UNION SELECT 'NUMERIC', CAST(CAST(625 AS NUMERIC(18, 5)) AS VARBINARY(25));

And this is what you should see in the results:

Next time we’ll look at floating points (FLOAT and REAL), and money (MONEY and SMALLMONEY).

Share your thoughts in the comments below.

Photo by Volkan Olmez on Unsplash.